At a recent NYU Shanghai Faculty Lunch Seminar Series, Visiting Professor Irith Hartman talked about, “Network Science: Connectivity and Vulnerability in the Modern World”. The following exchange grew out of that presentation .
What is beauty and simplicity in mathematics?
When asked a similar question, the renowned mathematician Paul Erdös put it this way, "Why are numbers beautiful? It's like asking why is Beethoven's Ninth Symphony beautiful. If you don't see why, someone can't tell you. I know numbers are beautiful. If they aren't beautiful, nothing is".
To me, what makes mathematics in general, and graph theory in particular, beautiful are its succinctness, simplicity, and depth. Graph theory is simple enough to explain to high school students, yet deep and profound enough to sustain the attention of some of the world’s smartest people. There are many problems and conjectures in graph theory that are easy to state, yet very difficult to solve. When drawn pictorially, they help us to understand intuitively the theory behind them. And although graph theory is a theoretical discipline, it has applications everywhere in our lives.
What are examples of the application of Graph Theory?
Graphs are used in a variety of ways to model many kinds of relations between objects and processes all around us. For instance, a transportation network, a social network and the Web are all graphs. The navigation application on a cell phone is based on algorithms for finding a shortest path in a graph. Designing integrated circuits, which are the building blocks of our computers, relies too on graph-theory. Finding out who are the opinion leaders in society, or how diseases spread, or how to find a good match between medical interns looking for hospital internships and hospitals recruiting interns – these are all problems in graph theory.
Can you tell me more about the problem of matching medical interns and hospitals?
In 2012, Lloyd Shapley received a Nobel Prize in economics for his work related to Graph Theory's so-called "stable marriage" problem. With his colleague, D. Gale, he was able to show how to guarantee a stable matching between, for instance, interns and hospitals so that each intern is assigned a unique hospital position, and vice versa, such that no intern or hospital can be found who would prefer each other over their current match.
Graphs can be visually stunning. How much do they reveal about the world we live in?
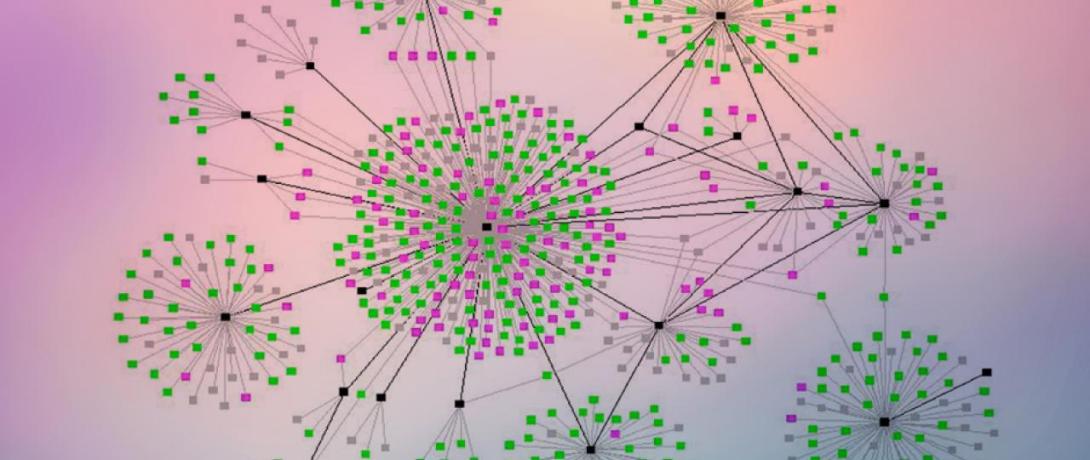
It is important, first, to distinguish between the graphs that we studied in high school, plotting in the x-y coordinates, and the graphs that are studied in “graph theory”. Even though they share the same name, these are different notions. The graphs I speak of are also known as networks. They have nodes with various connections, or“edges” that represent a binary relation between two given nodes. Graphs (or networks) are a method of modeling the world; they are an abstraction of the world. For example, the map of the subway, or the network representation of the Web are graphs.
Once a graph is defined, we can use theoretical tools to analyze it and hopefully, better understand the world we live in. The visualization of the graph can also reveal some interesting properties about it, but does not replace computational or theoretical work. In fact, different visualizations can reveal different properties, and hide others, so we have to be very clever and cautious about the visualization techniques that we use.
What were you looking for when you “stepped into” the messiness of the world?
After years of doing theoretical research on my own, I decided it would be more fun to work with other people. So when the opportunity came up to work on a large European mobility project, I grabbed it with both hands. While I did not ‘dirty my hands’ too much with collecting or analyzing data, I looked for problems that could be solved using graph theoretical tools. I worked on the challenge of designing a car sharing system for people commuting between work and home. Looking at it as an optimization problem, I tried to squeeze as many people in a car as possible. Later I realized that there is a gap between reality and mathematics. It is hard to convince two people to share a car, let alone five. There is the extra satisfaction that my algorithms may, some day, help in encouraging people to share rides to work.
Why did you initially choose to work on theoretical problems? Are real-life problems inherently different than theoretical problems?
Your question reminds me of a joke: What is the difference between Theory and Practice? In Theory, there is no difference…
I did my Ph.D. on a theoretical problem in graph theory, an open conjecture, which was considered difficult and beautiful. This is often what theoreticians do. We try to solve problems because they may lead to a better understanding of other theoretical problems. Sometimes, we do so just because they are challenging, because the problems are there… There are no practical considerations involved, no thoughts about possible applications. Later on, however, years or decades or even centuries later, some of these theoretical results may have real-life applications. So theory does not necessarily lead to practice, but most applications have some theory behind them.
Coming back to your presentation about networks, what do Facebook, Hollywood actors, yeast protein interaction, the airline and road network, and the email network have in common?
They can all be modeled and explained by a graph. However, all the examples that you gave, except for the road network, have an extra special property, that they are, what we call, ‘scale-free’ networks. Roughly speaking, they share the characteristic of having relatively few nodes with very high degree (many connections) and many nodes with small degree. In the Hollywood graph, that means that relatively fewer actors have acted in films with many other actors, but most actors have worked with few others. This property was discovered by L. Barabasi and it can be explained by the rule, “the rich get richer”. If you are an actor or a film director, you prefer to work with other famous actors than with less well known ones. Likewise, you are more likely to walk into a busy restaurant than an empty one. It turns out that in many cases, Mother Nature also follows this rule, and a lot of naturally occurring graphs are scale-free!
How does Tai Chi fit in to everything?
Tai-chi looks simple (but it’s not), it is beautiful, precise, and has deep effects on our body/mind and wellbeing. Isn’t that just like mathematics?